
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=25, BC=15, CF:DF=3:2.
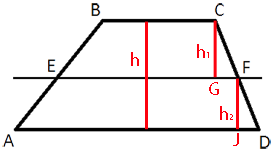 Проведем
высоты h1 и h2 как показано на рисунке.
Проведем
высоты h1 и h2 как показано на рисунке.
Рассмотрим треугольники CFG и FDJ.
∠CGF=∠FJD=90° (т.к. мы проводили
высоты).
∠CFG=∠FDJ (т.к. это
соответственные углы).
Следовательно, эти треугольники
подобны по
первому признаку подобия.
По
определению подобных треугольников:
CF/DF=CG/FJ=3/2
Для простоты обозначим:
CG=h1
FJ=h2
SEBCF=(CB+EF)*h1/2
SAEFD=(EF+AD)*h2/2
SABCD=(BC+AD)*(h1+h2)/2
Так сумма площадей этих
трапеций равна площади большой трапеции, то запишем:
(CB+EF)*h1/2+(EF+AD)*h2/2=(BC+AD)*(h1+h2)/2
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*(h1+h2)
(CB+EF)*h1+(EF+AD)*h2=(BC+AD)*h1+(BC+AD)*h2
(CB+EF)*h1-(BC+AD)*h1=(BC+AD)*h2-(EF+AD)*h2
(CB+EF-BC-AD)*h1=(BC+AD-EF-AD)*h2
(EF-AD)*h1=(BC-EF)*h2
h1/h2=(BC-EF)/(EF-AD)
3/2=(15-EF)/(EF-25)
3(EF-25)=2(15-EF)
3*EF-75=30-2*EF
5*EF=105
EF=21
Ответ: EF=21
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 2√
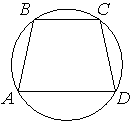 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=4/9, AB=18. Найдите AC.
 В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=10:9. Прямая AK пересекает сторону BC в точке P. Найдите отношение площади четырёхугольника KPCM к площади треугольника ABC.
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.


Комментарии: