Человек ростом 1,5 м стоит на расстоянии 7 м от столба, на котором висит фонарь на высоте 3,6 м. Найдите длину тени человека в метрах.
Рассмотрим рисунок:
BD - человек
AE - высота фонаря
ED - расстояние от фонаря до человека
DC - длина тени человека
Рассмотрим треугольники ACE и BCD.
∠C - общий
∠AEC=∠BDC=90° (это прямые углы)
Следовательно, по
первому признаку подобия треугольников, эти треугольники
подобны.
Тогда:
AE/BD=EC/DC
AE/BD=(ED+DC)/DC
3,6/1,5=(7+DC)/DC
2,4=7/DC+1
1,4=7/DC
DC=7/1,4=5
Ответ: длина тени равна 5 м.
Поделитесь решением
Присоединяйтесь к нам...
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
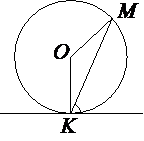Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
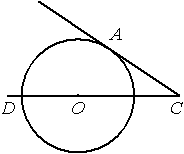Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
140°.
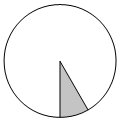Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-17 23:47:27) Администратор: Настя, решайте побольше задач.
(2017-01-16 17:58:59) настя: ка выучить геометрию с алгеброй?