На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 3 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
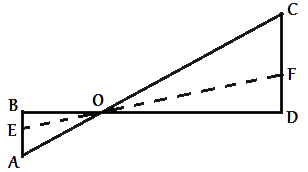Рисунок,предложенный в задаче можно условно перерисовать в виде треугольников. Рассмотрим треугольники ABO и COD.
1) /BOA=/DOC, т.к. они
вертикальные.
2) /OBA=/ODC=90°
3) /BAO=/DCO, т.к. они
внутренние накрест-лежащие.
Следовательно, треугольники ABO и COD
подобны (по признаку подобия). Отсюда следует, что CO/AO=CD/AB. Поэтому при движении, высота концов журавля будет подчиняться этой же пропорции.
CO/AO=CD/AB=CF/AE
6/3=CF/1,5 => CF=6*1,5/3=3.
Ответ: конец длинного плеча опустится на 3 метра.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=48 и CH=2. Найдите cosB.
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
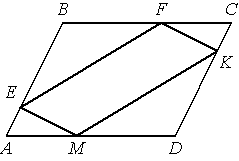В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём BF = DM, BE = DK. Докажите, что EFKM — параллелограмм.
В треугольнике ABC известно, что ∠BAC=62°, AD — биссектриса. Найдите угол BAD. Ответ дайте в градусах.
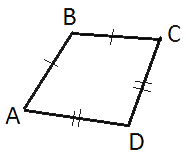В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: