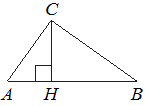
На гипотенузу AB прямоугольного треугольника ABC опущена высота CH, AH=4, BH=64. Найдите CH.
Вариант №1 (предложил пользователь Полина)
Рассмотрим треугольники ACH и BCH.
Докажем, что это подобные треугольники:
∠AHC=∠BHC=90° (так как CH -
высота).
По
теореме о сумме углов треугольника:
180°=∠CAH+∠AHC+∠HCA
180°=∠CAH+90°+∠HCA
90°=∠CAH+∠HCA
∠CAH=90°-∠HCA
Заметим, что:
∠BCH=90°-∠HCA
Получается, что ∠CAH=∠BCH
Тогда, по первому признаку подобия, данные треугольники подобны, т.е. можем записать пропорцию:
AH/CH=CH/BH
AH*BH=CH2
4*64=CH2
256=CH2
CH=√256=16
Ответ: 16
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC проведена биссектриса AL, угол ALC равен 148°, угол ABC равен 132°. Найдите угол ACB. Ответ дайте в градусах.
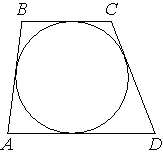Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 10,5 см, а длина – 36 см. Найдите расстояние между точками A и B (в метрах).
Радиус вписанной в квадрат окружности равен 14√
Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2020-05-12 15:27:02) Администратор: Александра, здравствуйте! Тоже хорошее решение, спасибо!
(2020-05-05 06:57:13) Александра: Здравствуйте, есть же еще решение без использования подобия треугольников. Провести медиану из прямого угла BM. Мы знаем, что медиана проведенная из прямого угла равна половине гипотенузы (BM=1/2*AB=34). И можем рассчитать отрезок между высотой и медианой(HM). HM=BH-1/2*AB=64-34=30. И по теореме Пифагора найдем CH^2=BM^2-HM^2=34^2-30^2=256 -> CH=16
(2017-11-13 20:46:51) Администратор: Полина, Ваш вариант проще, поэтому я опубликовал его. Спасибо за подсказку!
(2017-11-10 09:45:48) Полина: А зачем так усложнять? Можно же использовать свойство подобных треугольников. Составить пропорцию и решить в одно действие. CH²=64*4