Радиус окружности, описанной около квадрата, равен 16√
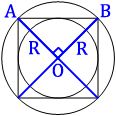Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(16√
AB2=2*162*2
AB2=162*22=(16*2)2=322
AB=32
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
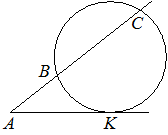Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Стороны AC, AB, BC треугольника ABC равны 2√
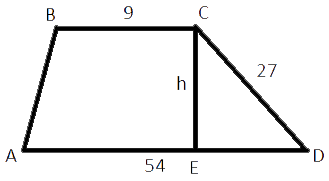Основания трапеции равны 9 и 54, одна из боковых сторон равна 27, а косинус угла между ней и одним из оснований равен √
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-09-27 16:06:12) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и мы ее обязательно добавим.
(2021-05-06 18:04:57) : периметр ромба 24 а один из углов равен 30 найдите площадьэтого ромба