Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
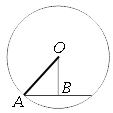Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Рассмотрим треугольник AOB.
Данный треугольник
прямоугольный, так как расстояние ОВ является
высотой (кротчайшее расстояние).
AB равна половине длины
хорды (по
третьему свойству хорды).
Тогда, по
теореме Пифагора:
AO2=OB2+AB2
AO2=242+(140/2)2
AO2=576+4900=5476
AO=74 - это радиус окружности, следовательно, диаметр D=2*AO=2*74=148
Ответ: 148
Поделитесь решением
Присоединяйтесь к нам...
Прямая касается окружности в точке K. Центр окружности – точка O. Хорда KM образует с касательной угол, равный 40°. Найдите величину угла KOM. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Существует квадрат, который не является прямоугольником.
2) Если два угла треугольника равны, то равны и противолежащие им стороны.
3) Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.
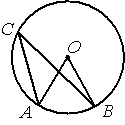Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
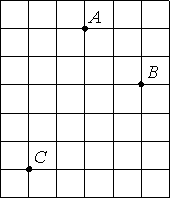На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 40:1, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 30.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: