Углы при одном из оснований трапеции равны 77° и 13°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 11 и 10. Найдите основания трапеции.
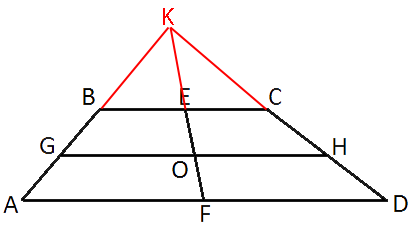Продлим стороны AB и CD до пересечения в точке K.
Рассмотрим треугольник AKD.
По
теореме о сумме углов треугольника:
∠AKD+∠KDA+∠DAK=180°
∠AKD+13°+77°=180°
∠AKD=90°
Следовательно треугольник AKD -
прямоугольный с гипотенузой AD.
KF -
медиана (по условию задачи).
Мысленно опишем вокруг этого треугольника окружность. Так как треугольник
прямоугольный, то центр окружности располагается на середине гипотенузы AD (по
теореме об описанной окружности).
Следовательно AF=FD=R - радиус окружности,
медиана KF тоже равна радиусу и, следовательно, равна AD/2.
Рассмотрим треугольник GKH.
Для этого треугольника KO -
медиана и равна половине гипотенузы GH (как и у предыдущего треугольника).
KO=OH=GH/2
В треугольнике BKC - аналогичная ситуация: KE=EC=BC/2
Вернемся к треугольнику GKH:
KO=OH=GH/2=11/2=5,5
5,5=OH=KE+EO
KE=EC (это мы выяснили ранее)
EO=EF/2 (так как EF делится пополам отрезком GH по условию задачи)
Следовательно, можем записать:
5,5=OH=KE+EO=EC+EF/2
EC=5,5-EF/2=5,5-10/2=0,5
BC=2*EC=2*0,5=1
Рассмотрим трапецию ABCD.
GH -
средняя линия, следовательно GH=(BC+AD)/2
2GH=BC+AD
AD=2GH-BC=2*11-1=22-1=21
Ответ: AD=21, BC=1
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=16, BC=15.
Стороны AC, AB, BC треугольника ABC равны 3√
Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
Наклонная крыша установлена на трёх вертикальных опорах, расположенных на одной прямой. Средняя опора стоит посередине между малой и большой опорами (см. рис.). Высота малой опоры 1,8 м, высота большой опоры 2,8 м. Найдите высоту средней опоры.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-17 22:31:53) Администратор: Катерина, я добавил несколько строк в решение, чтобы стало понятно, откуда взялось это равенство.
(2017-05-17 06:21:34) Катерина: Почему OH=EC+EF/2 ?