ОГЭ, Математика. Геометрия: Задача №F33966 | Ответ-Готов 


Юмор

Автор: Таська
Так выглядит современная программа обучения.
...читать далее

ОГЭ/ГИА

ЕГЭ (базовый уровень)

Числа и вычисления

Алгебраические выражения

Уравнения и неравенства

Числовые последовательности

Функции

Координаты на прямой и плоскости

Геометрия

Статистика и теория вероятностей

Алгебра

Уравнения и неравенства

Функции

Начала математического анализа

Геометрия

Элементы комбинаторики, статистики и теории вероятностей

ОГЭ, Математика.
Геометрия: Задача №F33966

Задача №615 из 1087
Условие задачи:

В треугольнике ABC AC=35, BC=5√15, угол C равен 90∘. Найдите радиус описанной окружности этого треугольника.

Решение задачи:

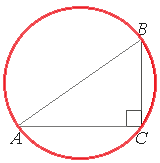Треугольник ABC - прямоугольный, тогда по теореме Пифагора:
AB2=AC2+BC2
AB2=352+(5√15)2
AB2=1225+25*15
AB2=1600
AB=40
Так как треугольник ABC прямоугольный, то это означает, что центр окружности находится на середине гипотенузы (по теореме об описанной окружности).
Тогда R=AB/2=40/2=20
Ответ: R=20

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела



Задача №2C468F

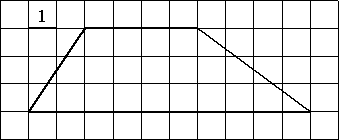Найдите площадь трапеции, изображённой на рисунке.



Задача №56179A

Стороны AC, AB, BC треугольника ABC равны 2√3, √7 и 1 соответственно. Точка K расположена вне треугольника ABC, причём отрезок KC пересекает сторону AB в точке, отличной от B. Известно, что треугольник с вершинами K, A и C подобен исходному. Найдите косинус угла AKC, если /KAC>90°.



Задача №160953

Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?



Задача №0A3F51

В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.



Задача №F0BC63

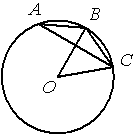Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).

Комментарии:



Найти задачу

По номеру с сайта fipi.ru (шестизначный номер из букв и цифр)
По порядковому номеру в текущем разделе
(от 1 до 1087)
По словам
Искать во всех разделах

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки
X Прямоугольный треугольник — это треугольник, в котором один угол прямой (то есть составляет 90°).
Сторона, противоположная прямому углу, называется гипотенузой (сторона c на рисунке).
Стороны, прилегающие к прямому углу, называются катетами.
X

Задайте вопрос по этой задаче.

Ваше имя:


Рейтинг@Mail.ru Copyright otvet-gotov.ru 2014-2021. Все права защищены. Яндекс.Метрика