
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ566 –Є–Ј 1087 |
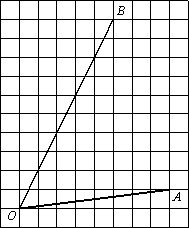 –Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ AOB.
–Э–∞–є–і–Є—В–µ —В–∞–љ–≥–µ–љ—Б —Г–≥–ї–∞ AOB.
–Т–∞—А–Є–∞–љ—В вДЦ1 (–Я—А–Є—Б–ї–∞–ї –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—М –Х–≤–≥–µ–љ–Є–є)
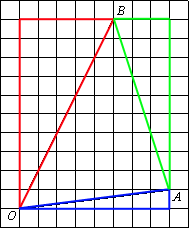 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AB.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї AB.
–Э–∞–є–і–µ–Љ –Ї–∞–ґ–і—Г—О —Б—В–Њ—А–Њ–љ—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABO –њ–Њ
—В–µ–Њ—А–µ–Љ–µ –Я–Є—Д–∞–≥–Њ—А–∞:
AO2=82+12
AO2=64+1=65
AO=√
AB2=92+32
AB2=81+9=90
AB=√
BO2=102+52
BO2=100+25=125
BO=√
–Я–Њ
—В–µ–Њ—А–µ–Љ–µ –Ї–Њ—Б–Є–љ—Г—Б–Њ–≤:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
90=65+125-2√
-100=-2√
50=5√
10=√
10=5√
2=√
cos∠AOB=2/√
–Я–Њ –Њ—Б–љ–Њ–≤–љ–Њ–є —В—А–Є–≥–Њ–љ–Њ–Љ–µ—В—А–Є—З–µ—Б–Ї–Њ–є —Д–Њ—А–Љ—Г–ї–µ:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(2/√
sin2∠AOB+4/13=1
sin2∠AOB=1-4/13
sin2∠AOB=13/13-4/13
sin2∠AOB=(13-4)/13
sin2∠AOB=9/13
sin∠AOB=3/√
tg∠AOB=sin∠AOB/cos∠AOB=(3/√
–Ю—В–≤–µ—В: tg∠AOB=1,5
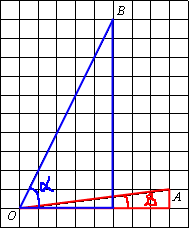 –Ф–Њ—Б—В—А–Њ–Є–Љ —З–µ—А—В–µ–ґ –і–Њ –і–≤—Г—Е
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Э–∞–є–і–µ–Љ
—В–∞–љ–≥–µ–љ—Б—Л –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–ї—П –Є—Е —Г–≥–ї–Њ–≤ –Ю.
–Ф–Њ—Б—В—А–Њ–Є–Љ —З–µ—А—В–µ–ґ –і–Њ –і–≤—Г—Е
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ—Л—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤. –Э–∞–є–і–µ–Љ
—В–∞–љ–≥–µ–љ—Б—Л –і–ї—П –Њ–±–Њ–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ –і–ї—П –Є—Е —Г–≥–ї–Њ–≤ –Ю.–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ
60¬∞, –∞ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 6.
–Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ
60¬∞, –∞ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 6.
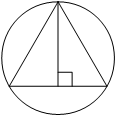 –†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —А–∞–≤–µ–љ 6. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
–†–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї–Њ–ї–Њ —А–∞–≤–љ–Њ—Б—В–Њ—А–Њ–љ–љ–µ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, —А–∞–≤–µ–љ 6. –Э–∞–є–і–Є—В–µ –≤—Л—Б–Њ—В—Г —Н—В–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AB=CD, AC=AD –Є ∠ABC=95¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї CAD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AB=CD, AC=AD –Є ∠ABC=95¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї CAD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
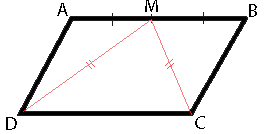 –Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD —В–Њ—З–Ї–∞ M вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AB. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ MC=MD. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
–Т –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–µ ABCD —В–Њ—З–Ї–∞ M вАФ —Б–µ—А–µ–і–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AB. –Ш–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ MC=MD. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –і–∞–љ–љ—Л–є –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ вАФ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
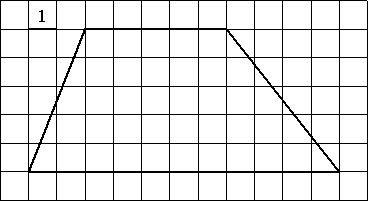 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2015-05-26 17:23:49) 2 –≤–∞—А–Є–∞–љ—В —Н—В–Њ: –Р–љ–∞–ї–Є—В–Є—З–µ—Б–Ї–∞—П –≥–µ–Њ–Љ–µ—В—А–Є—П —Г–ґ–µ
(2015-02-25 14:27:47) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –°–≤–µ—В–ї–∞–љ–∞, –Є–љ—В–µ—А–µ—Б–љ—Л–є –њ–Њ–і—Е–Њ–і, –њ—А–Є—Б—Л–ї–∞–є—В–µ –љ–∞ zapros@otvet-gotov.ru. –Ю–±—П–Ј–∞—В–µ–ї—М–љ–Њ –Є–Ј—Г—З—Г –Є –Њ–њ—Г–±–ї–Є–Ї—Г—О –Т–∞—И –≤–∞—А–Є–∞–љ—В.
(2015-02-25 13:47:48) –°–≤–µ—В–ї–∞–љ–∞: –Ь–Њ–ґ–љ–Њ –љ–∞–є—В–Є —З–µ—А–µ–Ј —Б–Ї–∞–ї—П—А–љ–Њ–µ –њ—А–Њ–Є–Ј–≤–µ–і–µ–љ–Є–µ –≤–µ–Ї—В–Њ—А–Њ–≤ –Ю–Р(8;1) –Є –Ю–Т(5;10),–µ—Б–ї–Є –њ–Њ–Љ–µ—Б—В–Є—В—М —В.–Ю –≤ –љ–∞—З–∞–ї–Њ –Ї–Њ–Њ—А–і–Є–љ–∞—В .–Э–∞ –Ї–∞–Ї–Њ–є –∞–і—А–µ—Б –Љ–Њ–ґ–љ–Њ –њ—А–Є—Б—Л–ї–∞—В—М —Б–≤–Њ–Є –≤–∞—А–Є–∞–љ—В—Л —А–µ—И–µ–љ–Є—П?
(2015-01-19 00:12:30) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –†–∞–Є—Б–∞, –Є–Ј–љ–∞—З–∞–ї—М–љ–Њ, –≤—В–Њ—А–Њ–є –≤–∞—А–Є–∞–љ—В –±—Л–ї –µ–і–Є–љ—Б—В–≤–µ–љ–љ—Л–Љ, –љ–Њ –Љ–љ–µ –њ–Є—Б–∞–ї–Є, —З—В–Њ —Н—В–∞ —Д–Њ—А–Љ—Г–ї–∞ –і–µ–≤—П—В–Є–Ї–ї–∞—Б—Б–љ–Є–Ї–∞–Љ –љ–µ–Є–Ј–≤–µ—Б—В–љ–∞. –Ю–і–Є–љ –Є–Ј –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї–µ–є –њ—А–Є—Б–ї–∞–ї –і—А—Г–≥–Њ–є –≤–∞—А–Є–∞–љ—В. –Ю–љ –і–ї–Є–љ–љ–µ–µ, –љ–Њ –Ј–∞—В–Њ –Њ—Б–љ–Њ–≤–∞–љ –љ–∞ –Є–Ј–≤–µ—Б—В–љ—Л—Е –≤ –і–µ–≤—П—В–Њ–Љ –Ї–ї–∞—Б—Б–µ —В–µ–Њ—А–µ–Љ–∞—Е, –њ–Њ—Н—В–Њ–Љ—Г —П –њ–Њ—Б—З–Є—В–∞–ї, —З—В–Њ –љ—Г–ґ–љ–Њ –њ–Њ–Ї–∞–Ј–∞—В—М –Њ–±–∞ –≤–∞—А–Є–∞–љ—В–∞.
(2015-01-18 10:48:07) –†–∞–Є—Б–∞: –°–њ–∞—Б–Є–±–Њ, –≤—В–Њ—А–Њ–є –≤–∞—А–Є–∞–љ—В –њ—А–Њ—Й–µ, –≥–ї–∞–≤–љ–Њ–µ, —З—В–Њ–±—Л –Ј–љ–∞–ї–Є —Г—З–∞—Й–Є–µ—Б—П —Д–Њ—А–Љ—Г–ї—Г —В–∞–љ–≥–µ–љ—Б —А–∞–Ј–љ–Њ—Б—В–Є 2-—Е —Г–≥–ї–Њ–≤