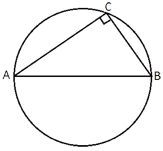
В треугольнике ABC AC=15, BC=5√
Треугольник ABC -
прямоугольный, тогда по
теореме Пифагора:
AB2=AC2+BC2
AB2=152+(5√
AB2=225+25*7
AB2=400
AB=20
Так как треугольник ABC прямоугольный, то это означает, что центр окружности находится на середине гипотенузы (по
теореме об описанной окружности).
Тогда R=AB/2=20/2=10
Ответ: R=10
Поделитесь решением
Присоединяйтесь к нам...
Точки M и N лежат на стороне AC треугольника ABC на расстояниях соответственно 9 и 11 от вершины A. Найдите радиус окружности, проходящей через точки M и N и касающейся луча AB, если cos∠BAC=√
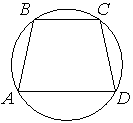Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
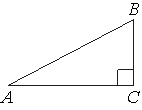В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AMD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: