Лестница соединяет точки A и B и состоит из 20 ступеней. Высота каждой ступени равна 16,5 см, а длина – 28 см. Найдите расстояние между точками A и B (в метрах).
Каждая ступенька представляет из себя
прямоугольный треугольник, следовательно расстояние между точками А и В будет равняться сумме гипотенуз ступеней.
По
теореме Пифагора:
Квадрат гипотенузы ступени равен 16,52+282=272,25+784=1056,25
Тогда длина гипотенузы равна √
Ответ: расстояние между точками A и B составляет 6,5 метра.
Поделитесь решением
Присоединяйтесь к нам...
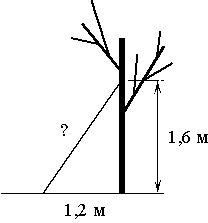Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB. Найдите площадь трапеции DAEC.
Медиана равностороннего треугольника равна 9√
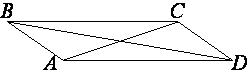В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
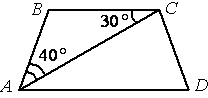Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: