
 Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
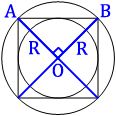 Проведем диаметры
описанной окружности, как показано на первом рисунке.
Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(4√2)2
AB2=2*16*2=64
AB=√64=8
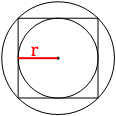 Проведем радиус
вписанной окружности, как на втором рисунке.
Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=8/2=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
 В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
В треугольнике ABC угол C прямой, BC=6, sinA=0,6. Найдите AB.
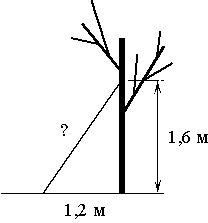 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 1,6 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.

Комментарии: