
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ818 –ł–∑ 1087 |
 –í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –ī–Ľ–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ AB=30, AC=100, —ā–ĺ—á–ļ–į O ‚ÄĒ —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ü—Ä—Ź–ľ–į—Ź BD, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AO, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É AC –≤ —ā–ĺ—á–ļ–Ķ D.
–Ě–į–Ļ–ī–ł—ā–Ķ CD.
–í —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–Ķ ABC –ł–∑–≤–Ķ—Ā—ā–Ĺ—č –ī–Ľ–ł–Ĺ—č —Ā—ā–ĺ—Ä–ĺ–Ĺ AB=30, AC=100, —ā–ĺ—á–ļ–į O ‚ÄĒ —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ–ĺ–Ľ–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ü—Ä—Ź–ľ–į—Ź BD, –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ–į—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ AO, –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—É AC –≤ —ā–ĺ—á–ļ–Ķ D.
–Ě–į–Ļ–ī–ł—ā–Ķ CD.
–ü—Ä–ĺ–≤–Ķ–ī–Ķ–ľ –ī–ĺ–Ņ–ĺ–Ľ–Ĺ–ł—ā–Ķ–Ľ—Ć–Ĺ—č–Ļ –ĺ—ā—Ä–Ķ–∑–ĺ–ļ –ł –≤–≤–Ķ–ī–Ķ–ľ –ĺ–Ī–ĺ–∑–Ĺ–į—á–Ķ–Ĺ–ł—Ź –ļ–į–ļ –Ņ–ĺ–ļ–į–∑–į–Ĺ–ĺ –Ĺ–į —Ä–ł—Ā—É–Ĺ–ļ–Ķ:
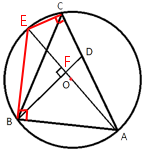 –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AEB –ł AFB.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AEB –ł AFB.
∠BAE - –ĺ–Ī—Č–ł–Ļ
–Ę—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ AEB - –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ—č–Ļ, —ā.–ļ. —Ü–Ķ–Ĺ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł –Ľ–Ķ–∂–ł—ā –Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ —ć—ā–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į (
—ā–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ–Ī –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł)
–Ę.–Ķ. ∠EBA=90¬į
∠AFB=90¬į, —ā.–ļ. –Ņ–ĺ —É—Ā–Ľ–ĺ–≤–ł—é AD ⊥ AE
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ņ–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, –ī–į–Ĺ–Ĺ—č–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–Ę–ĺ–≥–ī–į:
AE/AB=AB/AF => AE*AF=AB2
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł AEC –ł AFD.
∠FAD - –ĺ–Ī—Č–ł–Ļ
∠ACE=90¬į, —ā.–ļ. AE - –ī–ł–į–ľ–Ķ—ā—Ä –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł (
—ā–Ķ–ĺ—Ä–Ķ–ľ–į –ĺ–Ī –ĺ–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł)
∠AFD=90¬į, —ā.–ļ. –Ņ–ĺ —É—Ā–Ľ–ĺ–≤–ł—é BD ⊥ AE
–°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ, –Ņ–ĺ
–Ņ–Ķ—Ä–≤–ĺ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É –Ņ–ĺ–ī–ĺ–Ī–ł—Ź —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤, –ī–į–Ĺ–Ĺ—č–Ķ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł
–Ņ–ĺ–ī–ĺ–Ī–Ĺ—č.
–Ę–ĺ–≥–ī–į:
AE/AD=AC/AF => AD=AE*AF/AC
–ü–ĺ–ī—Ā—ā–į–≤–Ľ—Ź–Ķ–ľ –≤—č—ą–Ķ –Ĺ–į–Ļ–ī–Ķ–Ĺ–Ĺ–ĺ–Ķ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–ĺ:
AD=AB2/AC=302/100=9
CD=AC-AD=100-9=91
–ě—ā–≤–Ķ—ā: 91
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ ABCD –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–į –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC. –Ę–ĺ—á–ļ–į O —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC. –†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł O –ī–ĺ —ā–ĺ—á–ļ–ł A –ł –Ņ—Ä—Ź–ľ—č—Ö AD –ł AC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č 10, 9 –ł 6. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD.
–í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ ABCD –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–į –ī–ł–į–≥–ĺ–Ĺ–į–Ľ—Ć AC. –Ę–ĺ—á–ļ–į O —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC. –†–į—Ā—Ā—ā–ĺ—Ź–Ĺ–ł—Ź –ĺ—ā —ā–ĺ—á–ļ–ł O –ī–ĺ —ā–ĺ—á–ļ–ł A –ł –Ņ—Ä—Ź–ľ—č—Ö AD –ł AC —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ —Ä–į–≤–Ĺ—č 10, 9 –ł 6. –Ě–į–Ļ–ī–ł—ā–Ķ –Ņ–Ľ–ĺ—Č–į–ī—Ć –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į ABCD.
 –†–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–į–Ņ–Ķ—Ü–ł—é, —Ä–į–≤–Ķ–Ĺ 24. –Ě–į–Ļ–ī–ł—ā–Ķ –≤—č—Ā–ĺ—ā—É —ć—ā–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
–†–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–į–Ņ–Ķ—Ü–ł—é, —Ä–į–≤–Ķ–Ĺ 24. –Ě–į–Ļ–ī–ł—ā–Ķ –≤—č—Ā–ĺ—ā—É —ć—ā–ĺ–Ļ —ā—Ä–į–Ņ–Ķ—Ü–ł–ł.
 –Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ BH, –Ķ—Ā–Ľ–ł PK=13.
–Ę–ĺ—á–ļ–į H —Ź–≤–Ľ—Ź–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ–ľ –≤—č—Ā–ĺ—ā—č BH, –Ņ—Ä–ĺ–≤–Ķ–ī–Ķ–Ĺ–Ĺ–ĺ–Ļ –ł–∑ –≤–Ķ—Ä—ą–ł–Ĺ—č –Ņ—Ä—Ź–ľ–ĺ–≥–ĺ —É–≥–Ľ–į B –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā –ī–ł–į–ľ–Ķ—ā—Ä–ĺ–ľ BH –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į–Ķ—ā —Ā—ā–ĺ—Ä–ĺ–Ĺ—č AB –ł CB –≤ —ā–ĺ—á–ļ–į—Ö P –ł K —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ. –Ě–į–Ļ–ī–ł—ā–Ķ BH, –Ķ—Ā–Ľ–ł PK=13.
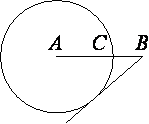 –Ě–į –ĺ—ā—Ä–Ķ–∑–ļ–Ķ AB –≤—č–Ī—Ä–į–Ĺ–į —ā–ĺ—á–ļ–į C —ā–į–ļ, —á—ā–ĺ AC=75 –ł BC=10. –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ A, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ C. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ł–∑ —ā–ĺ—á–ļ–ł B –ļ —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
–Ě–į –ĺ—ā—Ä–Ķ–∑–ļ–Ķ AB –≤—č–Ī—Ä–į–Ĺ–į —ā–ĺ—á–ļ–į C —ā–į–ļ, —á—ā–ĺ AC=75 –ł BC=10. –ü–ĺ—Ā—ā—Ä–ĺ–Ķ–Ĺ–į –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ A, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–į—Ź —á–Ķ—Ä–Ķ–∑ C. –Ě–į–Ļ–ī–ł—ā–Ķ –ī–Ľ–ł–Ĺ—É –ļ–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ–Ļ, –Ņ—Ä–ĺ–≤–Ķ–ī—Ď–Ĺ–Ĺ–ĺ–Ļ –ł–∑ —ā–ĺ—á–ļ–ł B –ļ —ć—ā–ĺ–Ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł.
 –í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź AD –ł BC —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 34 –ł 9, –į —Ā—É–ľ–ľ–į —É–≥–Ľ–ĺ–≤ –Ņ—Ä–ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł AD —Ä–į–≤–Ĺ–į 90¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł A –ł B –ł –ļ–į—Ā–į—é—Č–Ķ–Ļ—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ CD, –Ķ—Ā–Ľ–ł AB=10.
–í —ā—Ä–į–Ņ–Ķ—Ü–ł–ł ABCD –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź AD –ł BC —Ä–į–≤–Ĺ—č —Ā–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ 34 –ł 9, –į —Ā—É–ľ–ľ–į —É–≥–Ľ–ĺ–≤ –Ņ—Ä–ł –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–ł AD —Ä–į–≤–Ĺ–į 90¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –Ņ—Ä–ĺ—Ö–ĺ–ī—Ź—Č–Ķ–Ļ —á–Ķ—Ä–Ķ–∑ —ā–ĺ—á–ļ–ł A –ł B –ł –ļ–į—Ā–į—é—Č–Ķ–Ļ—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ–Ļ CD, –Ķ—Ā–Ľ–ł AB=10.

–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł:
(2020-05-05 17:14:49) –ź–ī–ľ–ł–Ĺ–ł—Ā—ā—Ä–į—ā–ĺ—Ä: –í–Ľ–į–ī, —ć—ā–ĺ –Ĺ–Ķ –Ī—Ä–Ķ–ī, –į –ĺ–Ņ–Ķ—á–į—ā–ļ–į. –ė—Ā–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ĺ!
(2020-05-05 16:53:07) –í–Ľ–į–ī: —á–Ķ –∑–į –Ī—Ä–Ķ–ī? –ļ–į–ļ –ĺ—ā—Ä–Ķ–∑–ļ–ł, –Ľ–Ķ–∂–į—Č–ł–Ķ –Ĺ–į –ĺ–ī–Ĺ–ĺ–Ļ —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ –ľ–ĺ–≥—É—ā –Ī—č—ā—Ć –Ņ–Ķ—Ä–Ņ–Ķ–Ĺ–ī–ł–ļ—É–Ľ—Ź—Ä–Ĺ—č?!?!?!