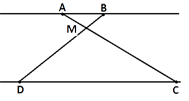Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=15, DC=30, AC=39.
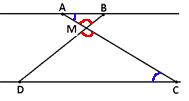Рассмотрим треугольники ABM и CDM.
∠AMB=∠CMD (так как они
вертикальные).
∠BAM=∠MCD (так как они
внутренние накрест-лежащие).
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, мы можем записать:
DC/AB=MC/AM
30/15=MC/AM
2=MC/AM
MC=2AM
AC=AM+MC (по рисунку)
39=AM+2AM
39=3AM
AM=13
MC=2AM=2*13=26
ответ: MC=26
Поделитесь решением
Присоединяйтесь к нам...
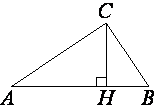В прямоугольном треугольнике
ABC катет AC=8, а высота CH, опущенная на гипотенузу, равна 2√
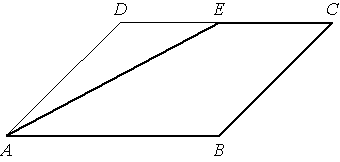Площадь параллелограмма
ABCD равна 56. Точка E — середина стороны
CD. Найдите площадь трапеции AECB.
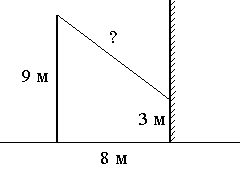От столба высотой 9 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 8 м. Вычислите длину провода.
Сторона ромба равна 20, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
В параллелограмм вписана окружность. Найдите периметр параллелограмма, если одна из его сторон равна 6.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: