
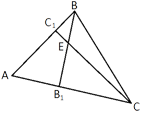 Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
 Проведем отрезок B1C1 и рассмотрим треугольники EB1C и EC1B.
Проведем отрезок B1C1 и рассмотрим треугольники EB1C и EC1B.
∠C1EB=∠B1EC (так как они
вертикальные).
∠EB1C=∠EC1B=90° (так как BB1 и CC1 -
высоты).
По
первому признаку подобия треугольников, рассматриваемые треугольники
подобны.
Следовательно:
EB1/EC1=EC/EB
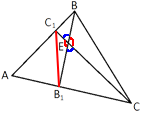
Рассмотрим треугольники EС1B1 и ECB
∠BEC=∠B1EC1 (так как они
вертикальные).
Как мы выяснили ранее:
EB1/EC1=EC/EB
Умножим левую и правую части равенства на EC1, получим:
EB1=EC1*EC/EB
Разделим левую и правую части на EC, получаем:
EB1/EC=EC1/EB
Получается, что по
второму признаку подобия треугольников, треугольники EС1B1 и ECB
подобны.
Следовательно, по
определению, углы BB1C1 и BCC1 равны.
Поделитесь решением
Присоединяйтесь к нам...
 Найдите площадь параллелограмма, изображённого на рисунке.
Найдите площадь параллелограмма, изображённого на рисунке.
Синус острого угла A треугольника ABC равен √
 Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
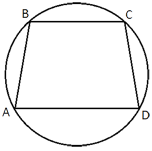 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
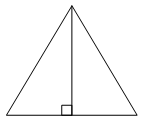 Высота равностороннего треугольника равна 15√
Высота равностороннего треугольника равна 15√

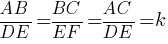
Комментарии: