
 В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
По условию задачи AB перпендикулярна BC, следовательно перпендикулярна и AD (т.к. в
трапеции основания параллельны).
Расстояние от точки Е до прямой CD - отрезок, перпендикулярный CD и проходящий через точку Е.
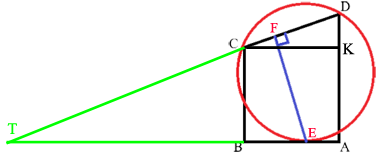 Продолжим стороны AB и CD до пересечения в точке T.
Продолжим стороны AB и CD до пересечения в точке T.
Проведем CK параллельно AB.
AK=BС (т.к. ABKC -
прямоугольник).
KD=AD-AK=14-12=2
По
определению косинуса: cos∠CDK=KD/CD=2/CD
Рассмотрим треугольники TCB и CKD.
∠CTB=∠DCK (т.к. это
соответственные углы при параллельных прямых TA и CK)
∠TBC=∠CKD=90°
Следовательно, эти треугольники
подобны (по
первому признаку подобия).
Тогда, BC/KD=TC/CD
12/2=TC/CD
TC=6CD
По
теореме о касательно и секущей:
TE2=TD*TC=(TC+CD)*TC=(6CD+CD)6CD=7CD*6CD=42CD2
TE=CD√
Рассмотрим треугольники TEF и TAD.
∠CTB - общий
∠EFT=∠TAD=90°
Следовательно, применив
теорему о сумме углов треугольника, получаем, что ∠TEF=∠ADT (=∠CDK).
Следовательно, cos∠TEF=cos∠ADT(=cos∠CDK).
EF=TE*cos∠TEF=TE*cos∠ADT=2TE/CD=2CD√
Ответ: EF=2√
Поделитесь решением
Присоединяйтесь к нам...
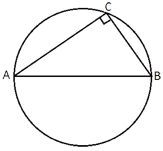
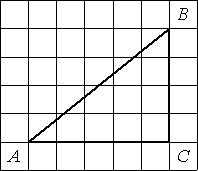 Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Найдите длину стороны AC, если радиус описанной окружности треугольника ABC равен 7.
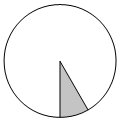 Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
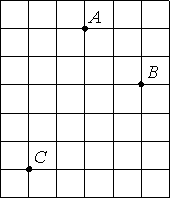 На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
На клетчатой бумаге с размером клетки 1см х 1см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.
 В треугольнике ABC AC=15, BC=5√
В треугольнике ABC AC=15, BC=5√

Комментарии:
(2017-06-03 19:47:21) Администратор: Катя, я подписал в решении, чтобы стало понятней. ∠ADT - это ∠CDK, который равен 2/CD (это мы нашли ранее).
(2017-06-03 01:35:19) Катя: Объясните пожалуйста последнюю строчку в решении : почему произведение косинуса угла ADT на TE равно 2TE/CD?