Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Рассмотрим треугольники ABC и MBN.
/B - общий.
/BAC=/BMN (т.к. это
соответственные углы)
/BCA=/BNM (т.к. это тоже
соответственные углы)
Следовательно, эти треугольники
подобны по
первому признаку подобия.
Тогда по
определению подобных треугольников:
AC/MN=BC/BN
AC/MN=BC/(BC-NC)
42/12=BC/(BC-25)
7/2=BC/(BC-25)
7(BC-25)=2BC
7BC-175=2BC
5BC=175
BC=35
BN=BC-NC=35-25=10
Ответ: BN=10
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь треугольника, изображённого на рисунке.
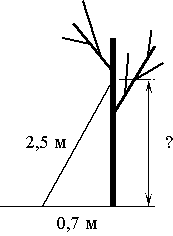Лестницу длиной 2,5 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 0,7 м?
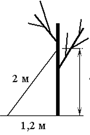Лестницу длиной 2 м прислонили к дереву.
На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на
1,2 м?
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
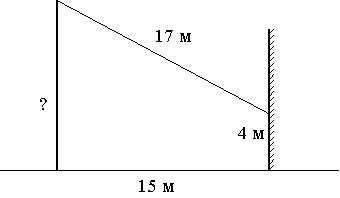От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Хочу получать новые решения
Ни какого спама
Автор: Таська
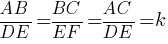
Комментарии: