Проектор полностью освещает экран A высотой 100 см, расположенный на расстоянии 230 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 320 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
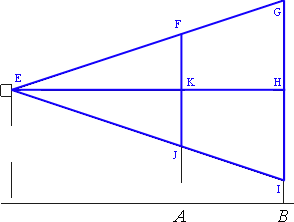Обозначим треугольники и их ключевые точки как показано на рисунке.
Рассмотрим треугольники EGI и EFJ.
Прямая EH перпендикулярна обоим экранам и проходит через их центр, следовательно является
серединным перпендикуляром.
То есть, FK=FJ/2=100/2=50 и GH=GI/2=320/2=160.
Рассмотрим треугольники EFK и EGH.
∠FEK - общий для обоих треугольников.
∠EKF=∠EHG=90° (т.к. EH -
серединный перпендикуляр).
Тогда, по
первому признаку подобия, данные треугольники
подобны.
Следовательно, мы можем записать пропорцию сторон:
EH/EK=GH/FK
EH/230=160/50
EH=(160*230)/50=736
Ответ: 736
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=12, AC=42, NC=25.
Катеты прямоугольного треугольника равны √
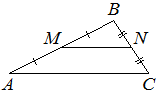Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
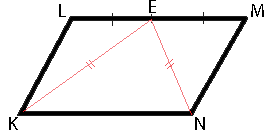В параллелограмме KLMN точка E — середина стороны LM. Известно, что EK=EN. Докажите, что данный параллелограмм — прямоугольник.
В трапеции ABCD AD=3, BC=1, а её площадь равна 12. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-02-10 10:23:50) ольга николаевна швецова: Спасибо!