Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит больший угол.
2) Любой прямоугольник можно вписать в окружность.
3) Площадь треугольника меньше произведения двух его сторон.
Рассмотрим каждое утверждение:
1) "Против большей стороны треугольника лежит больший угол" - это утверждение верно, по
теореме о соотношениях между сторонами и углами треугольника.
2) "Любой прямоугольник можно вписать в окружность" - это утверждение верно, так как, чтобы четырехугольник можно было вписать в окружность, должно выполняться условие - сумма противолежащих углов четырехугольника должна равняться 180°. Для Прямоугольника это условие выполняется.
3) "Площадь треугольника меньше произведения двух его сторон". Площадь треугольника можно вычислить по формуле Sтреугольника=1/2*a*b*sinC, где С - угол между сторонами a и b. Т.к. значение синуса не может быть больше единицы, получается, что a*b всегда больше 1/2*a*b*sinC. Поэтому это утверждение верно.
Ответ: 1), 2), 3)
Поделитесь решением
Присоединяйтесь к нам...
Прямые m и n параллельны. Найдите ∠3, если ∠1=6°, ∠2=101°. Ответ дайте в градусах.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 3 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
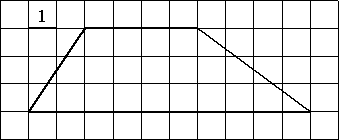Найдите площадь трапеции, изображённой на рисунке.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=40, AO=85.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: