
 Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
Радиус окружности, описанной около квадрата, равен 38√2. Найдите радиус окружности, вписанной в этот квадрат.
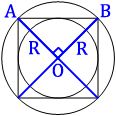 Проведем диаметры
описанной окружности, как показано на первом рисунке.
Проведем диаметры
описанной окружности, как показано на первом рисунке.
Очевидно, что
квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники
прямоугольные.
Тогда, по теореме Пифагора:
AB2=R2+R2
AB2=2R2
AB2=2(38√
AB2=2*382*2
AB2=382*22=(38*2)2=762
AB=76
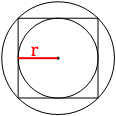 Проведем радиус
вписанной окружности, как на втором рисунке.
Проведем радиус
вписанной окружности, как на втором рисунке.
Очевидно, что:
r=AB/2=76/2=38
Ответ: 38
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, BC=8, sinA=0,4. Найдите AB.
 Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
Человек ростом 1,8 м стоит на расстоянии 6 м от столба, на котором висит фонарь на высоте 7,2 м. Найдите длину тени человека в метрах.
 Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
Радиус окружности, описанной около равностороннего треугольника, равен 10. Найдите высоту этого треугольника.
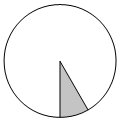 Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.

Комментарии: