
 Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
По
теореме об описанной окружности, центр описанной окружности лежит на точке пересечения
серединных перпендикуляров сторон треугольника.
У
прямоугольного треугольника центр окрудности лежит на середине гипотенузы, так же как и в треугольнике нашей задачи, следовательно данный треугольник
прямоугольный.
Следовательно, можно применить
теорему Пифагора:
AB2=BC2+AC2
AB - диаметр окружности, так как проходит через центр.
Тогда AB=2*R=2*10=20.
202=BC2+162
400=BC2+256
BC2=400-256=144
BC=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
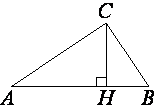 В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
В прямоугольном треугольнике ABC катет AC=25, а высота CH, опущенная на гипотенузу, равна 10√
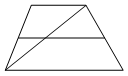 Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
 Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=7 и MB=9. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√

Комментарии: