
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ785 –Є–Ј 1087 |
 –С–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 12 –Є 20, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 2. –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л AB. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
–С–Њ–Ї–Њ–≤—Л–µ —Б—В–Њ—А–Њ–љ—Л AB –Є CD —В—А–∞–њ–µ—Ж–Є–Є ABCD —А–∞–≤–љ—Л —Б–Њ–Њ—В–≤–µ—В—Б—В–≤–µ–љ–љ–Њ 12 –Є 20, –∞ –Њ—Б–љ–Њ–≤–∞–љ–Є–µ BC —А–∞–≤–љ–Њ 2. –С–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ —Г–≥–ї–∞ ADC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Б–µ—А–µ–і–Є–љ—Г —Б—В–Њ—А–Њ–љ—Л AB. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є.
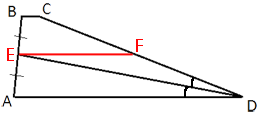 –Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–є –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ –Њ—В—А–µ–Ј–Њ–Ї, –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–є –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
EF -
—Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є, —В–∞–Ї –Ї–∞–Ї —Б–Њ–µ–і–Є–љ—П–µ—В —Б–µ—А–µ–і–Є–љ—Л –±–Њ–Ї–Њ–≤—Л—Е —Б—В–Њ—А–Њ–љ —В—А–∞–њ–µ—Ж–Є–Є (–њ–Њ
—В–µ–Њ—А–µ–Љ–µ –§–∞–ї–µ—Б–∞).
∠ADE=∠DEF (—В–∞–Ї –Ї–∞–Ї —Н—В–Њ
–љ–∞–Ї—А–µ—Б—В-–ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л –њ—А–Є –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л—Е –њ—А—П–Љ—Л—Е EF –Є AD –Є —Б–µ–Ї—Г—Й–µ–є ED).
–Я–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ ∠DEF=∠EDF (—В–∞–Ї –Ї–∞–Ї DE -
–±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞).
–Ч–љ–∞—З–Є—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї EFD -
—А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ—Л–є (–њ–Њ
—Б–≤–Њ–є—Б—В–≤—Г —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, EF=FD (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О).
EF=FD=CD/2=20/2=10
EF=(BC+AD)/2=10
(2+AD)/2=10
2+AD=20
AD=18
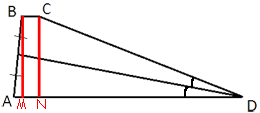 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Л –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Л –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
MN=BC=3 (—В.–Ї. BCNM -
–њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї).
BM=CN=h
–Ю–±–Њ–Ј–љ–∞—З–Є–Љ AM –Ї–∞–Ї x, –і–ї—П —Г–і–Њ–±—Б—В–≤–∞.
AD=AM+MN+ND
18=x+2+ND
ND=16-x
–Ф–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABM –Ј–∞–њ–Є—И–µ–Љ
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
AB2=h2+x2
122=h2+x2
h2=144-x2
–Ф–ї—П —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ CDN –Ј–∞–њ–Є—И–µ–Љ
—В–µ–Њ—А–µ–Љ—Г –Я–Є—Д–∞–≥–Њ—А–∞:
CD2=h2+ND2
202=h2+(16-x)2
400=h2+(16-x)2
–Я–Њ–і—Б—В–∞–≤–ї—П–µ–Љ –≤–Љ–µ—Б—В–Њ h2 –Ј–љ–∞—З–µ–љ–Є–µ –Є–Ј –њ–µ—А–≤–Њ–≥–Њ —Г—А–∞–≤–љ–µ–љ–Є—П:
400=144-x2+(16-x)2
400-144=-x2+162-2*16*x+x2
256=162-2*16*x |:16
16=16-2x
2x=0
x=0, –њ–Њ–ї—Г—З–∞–µ—В—Б—П, —З—В–Њ BM —Б–Њ–≤–њ–∞–і–∞–µ—В —Б–Њ —Б—В–Њ—А–Њ–љ–Њ–є AB, —В.–µ. AB —П–≤–ї—П–µ—В—Б—П –≤—Л—Б–Њ—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
–Ґ–Њ–≥–і–∞ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞:
S=AB(AD+BC)/2=12(18+2)/2=6*20=120
–Ю—В–≤–µ—В: 120
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –°—Г—Й–µ—Б—В–≤—Г–µ—В –Ї–≤–∞–і—А–∞—В, –Ї–Њ—В–Њ—А—Л–є –љ–µ —П–≤–ї—П–µ—В—Б—П –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ.
2) –Х—Б–ї–Є –і–≤–∞ —Г–≥–ї–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ—Л, —В–Њ —А–∞–≤–љ—Л –Є –њ—А–Њ—В–Є–≤–Њ–ї–µ–ґ–∞—Й–Є–µ –Є–Љ —Б—В–Њ—А–Њ–љ—Л.
3) –Т–љ—Г—В—А–µ–љ–љ–Є–µ –љ–∞–Ї—А–µ—Б—В –ї–µ–ґ–∞—Й–Є–µ —Г–≥–ї—Л, –Њ–±—А–∞–Ј–Њ–≤–∞–љ–љ—Л–µ –і–≤—Г–Љ—П –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–Љ–Є –њ—А—П–Љ—Л–Љ–Є –Є —Б–µ–Ї—Г—Й–µ–є, —А–∞–≤–љ—Л.
 –¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOB –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —Е–Њ—А–і—Г –Р–Т —В–∞–Ї, —З—В–Њ —Г–≥–Њ–ї –Ю–Р–Т —А–∞–≤–µ–љ 60¬∞. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л –Р–Т, –µ—Б–ї–Є —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 7.
–¶–µ–љ—В—А–∞–ї—М–љ—Л–є —Г–≥–Њ–ї AOB –Њ–њ–Є—А–∞–µ—В—Б—П –љ–∞ —Е–Њ—А–і—Г –Р–Т —В–∞–Ї, —З—В–Њ —Г–≥–Њ–ї –Ю–Р–Т —А–∞–≤–µ–љ 60¬∞. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г —Е–Њ—А–і—Л –Р–Т, –µ—Б–ї–Є —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 7.
 –Я—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ґ–Њ—З–Ї–∞ O вАФ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –•–Њ—А–і–∞ KM –Њ–±—А–∞–Ј—Г–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Г–≥–Њ–ї, —А–∞–≤–љ—Л–є 7¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OMK. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Я—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ґ–Њ—З–Ї–∞ O вАФ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –•–Њ—А–і–∞ KM –Њ–±—А–∞–Ј—Г–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Г–≥–Њ–ї, —А–∞–≤–љ—Л–є 7¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OMK. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Ь–µ–і–Є–∞–љ–∞ BM —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —П–≤–ї—П–µ—В—Б—П –і–Є–∞–Љ–µ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ–µ—А–µ—Б–µ–Ї–∞—О—Й–µ–є —Б—В–Њ—А–Њ–љ—Г BC –≤ –µ—С —Б–µ—А–µ–і–Є–љ–µ. –Ф–ї–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AC —А–∞–≤–љ–∞ 4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Ь–µ–і–Є–∞–љ–∞ BM —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —П–≤–ї—П–µ—В—Б—П –і–Є–∞–Љ–µ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ–µ—А–µ—Б–µ–Ї–∞—О—Й–µ–є —Б—В–Њ—А–Њ–љ—Г BC –≤ –µ—С —Б–µ—А–µ–і–Є–љ–µ. –Ф–ї–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AC —А–∞–≤–љ–∞ 4. –Э–∞–є–і–Є—В–µ —А–∞–і–Є—Г—Б –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
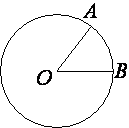 –Э–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ—В–Љ–µ—З–µ–љ—Л —В–Њ—З–Ї–Є A –Є B —В–∞–Ї, —З—В–Њ ∠AOB=66¬∞. –Ф–ї–Є–љ–∞ –Љ–µ–љ—М—И–µ–є –і—Г–≥–Є AB —А–∞–≤–љ–∞ 99. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –±–Њ–ї—М—И–µ–є –і—Г–≥–Є AB.
–Э–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ O –Њ—В–Љ–µ—З–µ–љ—Л —В–Њ—З–Ї–Є A –Є B —В–∞–Ї, —З—В–Њ ∠AOB=66¬∞. –Ф–ї–Є–љ–∞ –Љ–µ–љ—М—И–µ–є –і—Г–≥–Є AB —А–∞–≤–љ–∞ 99. –Э–∞–є–і–Є—В–µ –і–ї–Є–љ—Г –±–Њ–ї—М—И–µ–є –і—Г–≥–Є AB.

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: