На отрезке AB выбрана точка C так, что AC=60 и BC=27. Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.
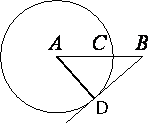Проведем отрезок AD, где D - точка касания
окружности и
касательной.
AD перпендикулярен к
касательной (по
свойству касательной), т.е. угол между AD и
касательной DB равен 90°.
Следовательно, треугольник ABD -
прямоугольный.
AD=AC=60 (т.к. это радиусы окружности и, соответственно, равны друг другу).
По
теореме Пифагора: AB2=AD2+BD2
(AC+BC)2=AD2+BD2
(60+27)2=602+BD2
7569=3600+BD2
BD2=3969
BD=63
Ответ: 63
Поделитесь решением
Присоединяйтесь к нам...
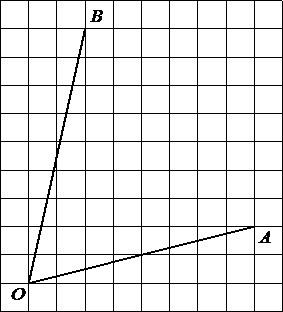Найдите тангенс угла
AOB.
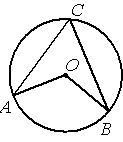Точка О – центр окружности, /AOB=130° (см. рисунок). Найдите величину угла
ACB (в градусах).
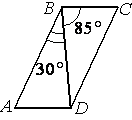Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 85° и 30°. Найдите меньший угол параллелограмма.
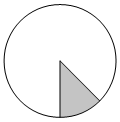Площадь круга равна 88. Найдите площадь сектора этого круга, центральный угол которого равен 45°.
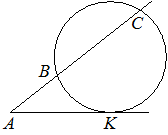Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=6, AC=54. Найдите AK.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: