
 Найдите площадь квадрата, если его диагональ равна 1.
Найдите площадь квадрата, если его диагональ равна 1.
 По
определению стороны
квадрата равны друг другу, обозначим длину сторон как "а".
По
определению стороны
квадрата равны друг другу, обозначим длину сторон как "а".
По
свойству, все углы квадрата прямые, следовательно можно применить
теорему Пифагора для получившегося треугольника, квадрат диагонали будет равен сумме квадратов сторон:
a2+a2=12
2a2=1
a2=0,5
a2 - это и есть площадь квадрата.
Ответ: 0,5
Поделитесь решением
Присоединяйтесь к нам...
 Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
Проектор полностью освещает экран A высотой 190 см, расположенный
на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.
 Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
 Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
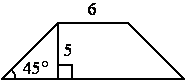 В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
В равнобедренной трапеции известны высота, меньшее основание и угол при основании. Найдите большее основание.
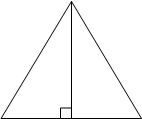 Высота равностороннего треугольника равна
15√
Высота равностороннего треугольника равна
15√

Комментарии: