Длина хорды окружности равна 140, а расстояние от центра окружности до этой хорды равно 24. Найдите диаметр окружности.
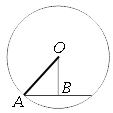Обозначим ключевые точки, как показано на рисунке. Проведем отрезок АО.
Рассмотрим треугольник AOB.
Данный треугольник
прямоугольный, так как расстояние ОВ является
высотой (кротчайшее расстояние).
AB равна половине длины
хорды (по
третьему свойству хорды).
Тогда, по
теореме Пифагора:
AO2=OB2+AB2
AO2=242+(140/2)2
AO2=576+4900=5476
AO=74 - это радиус окружности, следовательно, диаметр D=2*AO=2*74=148
Ответ: 148
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равностороннего треугольника совпадают.
2) Существует квадрат, который не является ромбом.
3) Сумма углов остроугольного треугольника равна 180°.
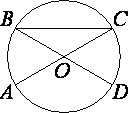В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 132°. Найдите вписанный угол ACB. Ответ дайте в градусах.
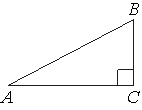В треугольнике ABC угол C равен 90°, tgB=7/6, BC=18. Найдите AC.
Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 9 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 20 см. Сколько потребуется таких дощечек?
Стороны AC, AB, BC треугольника ABC равны 2√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: