В треугольнике ABC угол C равен 90°, AC=6, tgA=2√
По
определению: tgA=BC/AC => BC=AC*tgA=6*2√
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(4√
AB2=16*10+36
AB2=196
AB=14
Ответ: AB=14
Поделитесь решением
Присоединяйтесь к нам...
Сторона ромба равна 8, а расстояние от точки пересечения диагоналей ромба до неё равно 2. Найдите площадь этого ромба.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
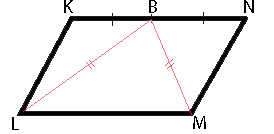В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
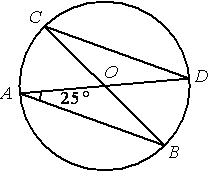В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-05-18 22:10:58) Администратор: Светлана, спасибо большое, исправлено.
(2015-05-18 20:33:43) Светлана: Ошибка в ответе. Корень из 196=14!