Катеты прямоугольного треугольника равны 2√
Так как треугольник
прямоугольный, то можем применить
теорему Пифагора:
AB2=BC2+AC2
AB2=12+(2√
AB2=1+4*6=25
AB=5
Меньший угол лежит напротив меньшей стороны, 1<2√
Ответ: 0,2
Поделитесь решением
Присоединяйтесь к нам...
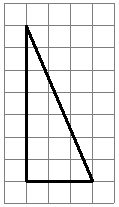На клетчатой бумаге с размером клетки 1×1 изображён прямоугольный треугольник. Найдите длину его большего катета.
Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
Одна из биссектрис треугольника делится точкой пересечения биссектрис в отношении 7:6, считая от вершины. Найдите периметр треугольника, если длина стороны треугольника, к которой эта биссектриса проведена, равна 48.
В трапеции ABCD известно, что AD=4, BC=3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: