В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
По
определению: sinA=BC/AB => BC=AB*sinA=AB*0,4=0,4AB
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(0,4AB)2+(√
AB2-(0,4AB)2=21
AB2(1-0,42)=21
AB2*0,84=21
AB2=25
AB=5
Ответ: AB=5
Поделитесь решением
Присоединяйтесь к нам...
Из вершины прямого угла C треугольника
ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
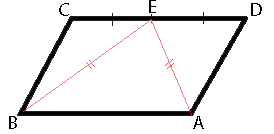В параллелограмме ABCD точка E — середина стороны CD. Известно, что EA=EB. Докажите, что данный параллелограмм — прямоугольник.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: