
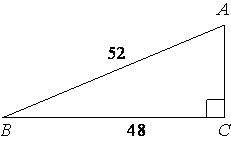 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Площадь прямоугольного треугольника S=AC*BC/2
Найдем AC по
теореме Пифагора:
AB2=AC2+BC2
522=AC2+482
AC2=2704-2304=400
AC=20
SABC=20*48/2=480
Ответ: SABC=480
Поделитесь решением
Присоединяйтесь к нам...
Имеются два сосуда, содержащие 10 кг и 16 кг раствора кислоты различной концентрации. Если их слить вместе, то получится раствор, содержащий 55% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 61% кислоты. Сколько килограммов кислоты содержится в первом растворе?
 Площадь прямоугольного треугольника равна 50√
Площадь прямоугольного треугольника равна 50√
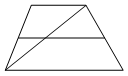 Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
Основания трапеции равны 8 и 18. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции одна из её диагоналей.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
 Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).

Комментарии: