Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.
∠GAE=∠BEA (т.к. они
накрест-лежащие)
∠GAE=∠BEA=∠BAE (т.к. AE -
биссектриса).
Получается, что треугольник ABE -
равнобедренный.
BF -
биссектриса, а по
свойству равнобедренного треугольника, она так же и
медиана и
высота.
Таким образом, получается, что треугольник ABF -
прямоугольный.
По
теореме Пифагора:
AB2=AF2+BF2
AB2=122+52
AB2=144+25=169
AB=13
Ответ: AB=13
Поделитесь решением
Присоединяйтесь к нам...
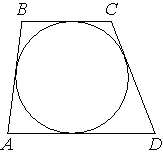Трапеция ABCD с основаниями AD и BC описана около окружности, AB=14, BC=8, CD=12. Найдите AD.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=88 и BC=BM. Найдите AH.
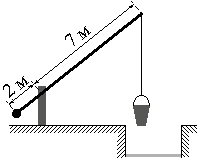На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 7 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=66, AC=44, MN=24. Найдите AM.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: