В треугольнике ABC угол C равен 90°, sinA=9/10, AC=√
По
определению: sinA=BC/AB => BC=AB*sinA=AB*9/10=0,9AB
По
теореме Пифагора:
AB2=BC2+AC2
AB2=(0,9AB)2+(√
AB2-(0,9AB)2=19
AB2(1-0,92)=19
AB2*0,19=19
AB2=100
AB=10
Ответ: AB=10
Поделитесь решением
Присоединяйтесь к нам...
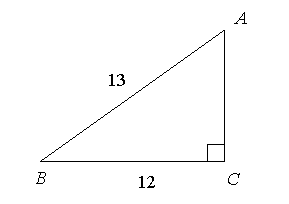Найдите площадь треугольника, изображённого на рисунке.
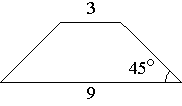В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Точка H является основанием высоты BH, проведённой из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: