В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
SABCD=EF*(AD+BC)/2=2000
PABCD=AB+BC+CD+AD=200
AB=CD (так как
трапеция равнобедренная).
Чтобы окружность можно было вписать в трапецию должно выполняться условие - суммы противоположных сторон трапеции должны быть равны, т.е.
AD+BC=AB+CD
AD+BC=2AB (т.к. AB=CD)
Тогда:
PABCD=AB+BC+CD+AD=AB+2AB+AB=4AB=200
AB=50
Значит, AD+BC=2*50=100
SABCD=EF*(AD+BC)/2=EF*100/2=EF*50=2000
EF=40
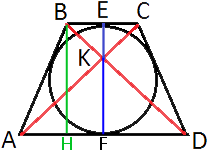Проведем
высоту BH, как показано на рисунке.
BH=EF=40, так как BEFH -
прямоугольник.
AH=(AD-BC)/2
По
теореме Пифагора:
AB2=BH2+AH2
502=402+AH2
2500=1600+AH2
900=AH2
30=AH=(AD-BC)/2
60=AD-BC, вспомним, что AD+BC=100
60=AD-(100-AD)
60=AD-100+AD
160=2AD
AD=80
Тогда BC=100-80=20
Рассмотрим треугольники AKF и CKE
AF=AD/2=40
CE=BC/2=10
∠AFK=∠CEK=90°
∠AKF=∠CKE (т.к. они
вертикальные)
По
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, AF/CE=KF/KE
40/10=KF/KE
4=(EF-KE)/KE (вспомним, что EF=40)
4KE=40-KE
5KE=40
KE=8
Ответ: KE=8
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника CMD.
ABCDEFGHIJ — правильный десятиугольник. Найдите угол CAH. Ответ дайте в градусах.
Периметр квадрата равен 184. Найдите площадь квадрата.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
Укажите номера верных утверждений.
1) Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, образованные этими сторонами, равны, то треугольники подобны.
2) Смежные углы равны.
3) Медиана равнобедренного треугольника, проведённая к его основанию, является его высотой.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: