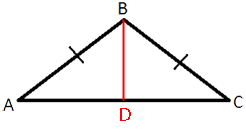
Боковая сторона равнобедренного треугольника равна 10, а основание равно 12. Найдите площадь этого треугольника.
Площадь треугольника равна a*h/2, где h -
высота треугольника, а - сторона треугольника, к которой проведена высота.
SABC=AC*BD/2
AD=DC=AC/2=12/2=6 (по
свойству равнобедренного треугольника высота является
медианой)
Тогда, по
теореме Пифагора:
AB2=BD2+AD2
102=BD2+62
100=BD2+36
BD2=64
BD=8
SABC=AC*BD/2=12*8/2=48
Ответ: SABC=48
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 67. Найдите площадь четырёхугольника ABMN.
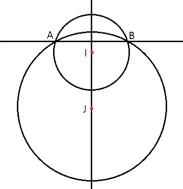Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
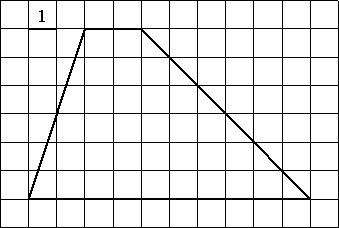Найдите площадь трапеции, изображённой на рисунке.
Лестница соединяет точки A и B. Высота каждой ступени равна 13 см, а длина – 84 см. Расстояние между точками A и B составляет 25,5 м. Найдите высоту, на которую поднимается лестница (в метрах).
Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-05-12 09:27:42) : квадрат со стороной 8 см описан около окружности. найдите площадь прямоугольного треугольника с острым углом 30, вписанного в данную окружность
(2014-05-17 14:33:39) Администратор: Танюшка, спасибо, хорошее логичное решение. Опубликуем в скором времени.
(2014-05-17 14:29:36) танюшка: Можно решить через теорему Герона. Боковые стороны равны между собой и равны 10.Находим полупериметр: р=(10+10+12)/2=16.Подставляем данные в формулу: S=√16(16-10)*(16-10)*(16-12); S=√64*36 ; S=8*6=48