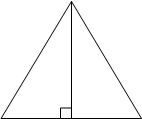
Высота равностороннего треугольника равна
15√
Обозначим сторону
равностороннего треугольника как a.
Высота является
медианой (по
свойству равностороннего треугольника), следовательно, высота делит сторону треугольника пополам.
Тогда, по
теореме Пифагора можем записать:
a2=(a/2)2+(15√
a2-(a/2)2=152*3
a2-a2/4=225*3
3a2/4=675
3a2=2700
a2=900
a=30
Так как все стороны равны, то периметр P=3*а=90
Ответ: P=90.
Поделитесь решением
Присоединяйтесь к нам...
Длина хорды окружности равна 130, а расстояние от центра окружности до этой хорды равно 72. Найдите диаметр окружности.
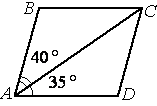Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 40° и 35°. Найдите больший угол параллелограмма.
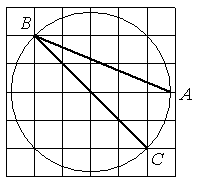Найдите угол ABC. Ответ дайте в градусах.
AC и BD – диаметры окружности с центром O. Угол ACB равен 74°. Найдите угол AOD. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-11-10 17:58:16) Администратор: Ирина, a2-a2/4=4a2/4-a2/4=(4a2-a2)/4=3a2/4, т.е. просто привели к общему знаменателю.
(2015-11-08 15:42:26) : Большое спасибо
(2015-11-08 15:15:50) Администратор: Ирина, a2-a2/4=4a2/4-a2/4=(4a2-a2)/4=3a2/4, т.е. просто привели к общему знаменателю.
(2015-11-08 15:09:28) Ирина: Скажите пожалуйста, откуда в четвертом действии 3a?