
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
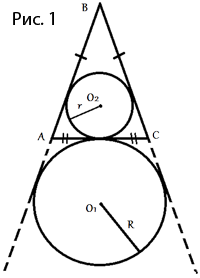 Проведем следующие отрезки (как показано на рисунке 2):
Проведем следующие отрезки (как показано на рисунке 2):
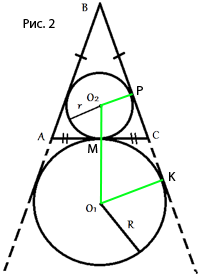 1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
1) Из точки О2 к точке касания окружности и продолжения стороны ВС. (точка Р)
2) Из точки О1 к точке касания окружности и продолжения стороны ВС. (Точка К)
3) Из точки О1 к точке О2.
Заметим, что:
1) СМ=АС/2.
2) СР=СМ, по
второму свойству касательной.
3) СМ=СК, по
второму свойству касательной.
4) O1O2=R+r.
5) O2Р перпендикулярна AC, по
первому свойству касательной.
6) O1К тоже перпендикулярна AC, по
свойству касательной.
7) Из пунктов 2) и 3) следует, что СР=СК=СМ=АС/2. Тогда РК=АС/2+АС/2=АС.
Следовательно, O2Р ||
O1К (по
свойству параллельных прямых). Отсюда следует, что
О1О2РК - прямоугольная трапеция (по
определению трапеции).
Рассмотрим эту трапецию.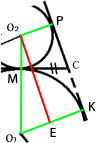
Проведем отрезок О2Е параллельный РК, а раз он параллелен РК, то в свою очередь перпендикулярен О1К и равен ему. Следовательно получившийся треугольник O1O2Е -
прямоугольный.
Тогда, по
теореме Пифагора, мы можем записать: (O1O2)2=(O2Е)2+(O1Е)2.
Подставим известные нам данные, полученные ранее:
(R+r)2=AC2+(R-r)2. Раскрываем скобки, получаем:
R2+2Rr+r2=AC2+R2-2Rr+r2
2Rr=AC2-2Rr
4Rr=AC2
r=(AC2)/4R
r=42/(4*2,5)
r=4/2,5
r=1,6
Ответ: радиус вписанной окружности равен 1,6.
Поделитесь решением
Присоединяйтесь к нам...
 Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
 Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=1 и HD=63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.
 Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Сторона ромба равна 30, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
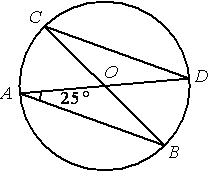 В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
В окружности с центром в точке О проведены диаметры AD и BC, угол OAB равен 25°. Найдите величину угла OCD.
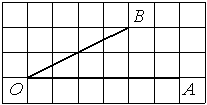 Найдите тангенс угла AOB, изображённого на рисунке.
Найдите тангенс угла AOB, изображённого на рисунке.

Комментарии: