Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 8,4, а AB=4.
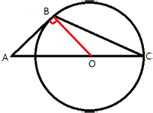Отрезок AC равен сумме отрезков AO и OC, OC - равен радиусу окружности, т.е.
OC=8,4/2=4,2. Найдем AO.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
AO2=42+4,22
AO2=16+17,64=33,64
AO=√33,64=5,8
AC=AO+OC=5,8+4,2=10
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
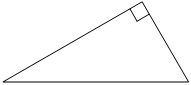Один из острых углов прямоугольного треугольника равен 57°. Найдите его другой острый угол. Ответ дайте в градусах.
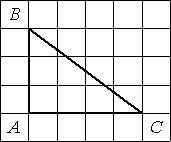Найдите тангенс угла С треугольника ABC, изображённого на рисунке.
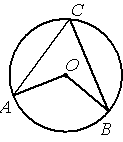Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
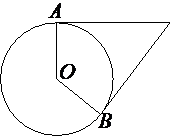Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
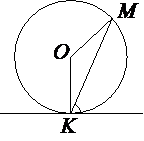Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: