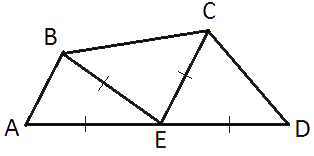
Середина E стороны AD выпуклого четырехугольника равноудалена от всех его вершин. Найдите AD, если BC=8, а углы B и C четырёхугольника равны соответственно 92° и 148°.
Вариант №1
Сумма углов любого выпуклого n-угольника равна (n-2)180, тогда сумма углов четырехугольника (4-2)180=360.
Т.е. ∠A+∠B+∠C+∠D=360
∠A+92°+148°+∠D=360°
∠A+∠D=120°
Треугольники AEB, BEC и ECD -
равнобедренные, т.к. стороны AE=EB=EC=ED.
Следовательно:
∠A=∠ABE
∠EBC=∠ECB
∠ECD=∠D
Использую сумму углов четырехугольника, запишем:
∠A+∠ABE+∠EBC+∠ECB+∠ECD+∠D=360°
Используя ранее полученные равенства, запишем:
∠A+∠A+2∠EBC+∠D+∠D=360°
2∠A+2∠EBC+2∠D=360°
∠A+∠EBC+∠D=180°
120°+∠EBC=180°
∠EBC=60°
Рассмотрим треугольник EBC.
По
теореме о сумме углов треугольника ∠BEC тоже равен 60°.
Следовательно треугольник EBC -
равносторонний (по
свойству).
Значит BC=BE=EC=8 (по
определению) и
8=BE=EC=AE (по условию задачи).
AD=AE+ED=8+8=16
Ответ: AD=16
Поделитесь решением
Присоединяйтесь к нам...
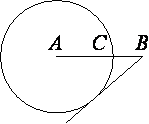На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
В трапеции ABCD известно, что AD=4, BC=3, а её площадь равна 84. Найдите площадь трапеции BCNM, где MN — средняя линия трапеции ABCD.
В треугольнике ABC известно, что AB=8, BC=10, AC=14. Найдите cos∠ABC.
В окружности с центром в точке O проведены диаметры AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
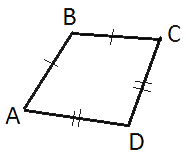В выпуклом четырехугольнике ABCD AB=BC, AD=CD, ∠B=100° , ∠D=104°. Найдите угол A . Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-28 21:55:05) Администратор: Alissa, хорошее решение, я решил опубликовать его от Вашего имени. Спасибо!
(2017-05-19 21:22:32) Alissa: Очевидно, что АВСD- четырёхугольник,вписанный в окружность. Значит сумма противолежащих углов А+С=В+D=180 градусам.Тогда угол D=180-92=88,угол ЕСD=88.По условию угол С=148,тогда угол ВСЕ=148-88=60.И треугольник ВСЕ равносторонний и т.д