Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Рассмотрим треугольник АОВ. АО=ОВ, т.к. это радиусы окружности. Следовательно,
треугольник АОВ - равнобедренный. Следовательно, /ОВА = /ОАВ (по свойству равнобедренного треугольника).
По теореме о сумме углов треугольника можем записать:
180°=/AOB+/OBA+/BAO
180°=60°+/OBA+/BAO
120°=/OBA+/BAO
А так как /OBA=/BAO, то /OBA=/BAO=120°/2=60°.
Следовательно треугольник АОВ - равносторонний (по свойству равностороннего треугольника). Следовательно, ОВ=ОА=АВ=4.
Ответ: АВ=4.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 146°. Найдите угол C . Ответ дайте в градусах.
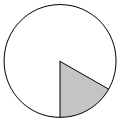Площадь круга равна 78. Найдите площадь сектора этого круга, центральный угол которого равен 60°.
Укажите номера верных утверждений.
1) Биссектриса равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали ромба точкой пересечения делятся пополам.
3) Из двух хорд окружности больше та, середина которой находится дальше от центра окружности.
В треугольнике ABC угол C равен 90°, tgB=3/4, BC=12. Найдите AC.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: