Углы B и C треугольника ABC равны соответственно 66° и 84°.
Найдите BC, если радиус окружности, описанной около треугольника ABC, равен 15.
Вариант №1
По
теореме о сумме углов треугольника:
180°=∠A+∠B+∠C
180°=∠A+66°+84°
∠A=180°-66°-84°=30°
По
теореме синусов:
2R=BC/sin∠A
2R=BC/sin30°=BC/(1/2)=2BC
R=BC=15
Ответ: 15
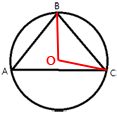Проведем два отрезка из центра к точкам B и C, как показано на рисунке.Поделитесь решением
Присоединяйтесь к нам...
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=15, AC=25, NC=22.
В трапеции ABCD AD=8, BC=5, а её площадь равна 13. Найдите площадь треугольника ABC.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:4, KM=13.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: