Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 48, а площадь равна 288.
Решение прислал пользователь Людмила
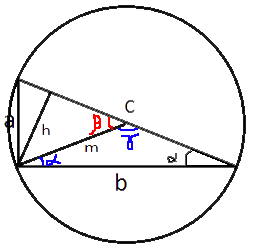Проведем из прямого угла медиану и высоту, обозначив их m и h соответственно.
Если описать окружность вокруг треугольника, то центр этой окружности будет лежать на середине гипотенузы (по
теореме об описанной окружности). Следовательно:
m=c/2=48/2=24
S=(1/2)hc
h=2S/c=2*288/48=288/24=12
По
определению синуса:
sinβ=h/m=12/24=0,5
По таблице определяем, что β=30°
Угол γ является внешнем к β, следовательно γ=180°-β=180°-30°=150°
Треугольник, содержащий угол γ,
равнобедренный, так как медиана m и половина гипотенузы равны (это мы выяснили ранее).
Следовательно, по
свойству равнобедренного треугольника углы при основании равны (обозначены α).
Тогда, по
теореме о сумме углов треугольника:
180°=γ+α+α
180°=150°+2α
α=15° - это один из искомых углов.
Другой искомый угол найдем по той же
теореме об углах треугольника: 180°-90°-15°=75°
ответ: 15° и 75°
Поделитесь решением
Присоединяйтесь к нам...
Какие из следующих утверждений верны?
1) Один из двух смежных углов острый, а другой тупой.
2) Площадь квадрата равна произведению двух его смежных сторон.
3) Все хорды одной окружности равны между собой.
В треугольнике ABC угол C равен 90°, sinB=5/17, AB=51. Найдите AC.
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АВ, если сторона АС равна 4.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 8 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: