В треугольнике ABC AB=BC=37, AC=24. Найдите длину медианы BM.
По условию задачи треугольник ABC -
равнобедренный.
BM является не только
медианой, но и
высотой (по
третьему свойству равнобедренного треугольника).
Следовательно:
1) AM=MC=AC/2=24/2=12
2) Треугольник ABM
прямоугольный.
Тогда, по
теореме Пифагора:
AB2=BM2+AM2
372=BM2+122
1369=BM2+144
BM2=1225
BM=35
Ответ: 35
Поделитесь решением
Присоединяйтесь к нам...
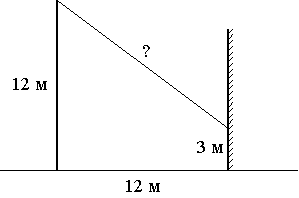От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник ACP, равен 12 см, тангенс угла ABC равен 2,4. Найдите радиус вписанной окружности треугольника ABC.
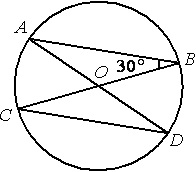В окружности с центром в точке О проведены диаметры AD и BC, угол
ABO равен 30°. Найдите величину угла ODC.
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 57.
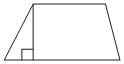Основания трапеции равны 5 и 13, а высота равна 9. Найдите площадь этой трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: