
 Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Диагональ прямоугольника образует угол 50° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
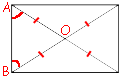 Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
Диагонали
прямоугольника равны и точкой пересечения делятся пополам (по
свойству прямоугольника).
Рассмотрим треугольник ABO (см. рисунок).
AO=BO (как мы только что выяснили).
Следовательно, треугольник ABO -
равнобедренный.
По первому
свойству равнобедренного треугольника:
∠OBA=∠OAB
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OBA+∠OAB
180°=∠AOB+50°+50°
∠AOB=80°
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
 Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
Тангенс острого угла прямоугольной трапеции равен 2/9. Найдите её большее основание, если меньшее основание равно высоте и равно 54.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
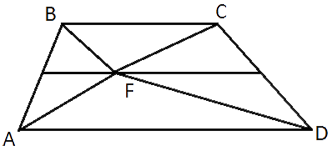 На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.
 Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и ADB подобны.
 В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 4. Найдите площадь трапеции.

Комментарии: