
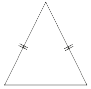
 Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
Боковая сторона равнобедренного треугольника равна 25, а основание равно 30. Найдите площадь этого треугольника.
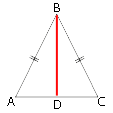 Проведем высоту BD.
Проведем высоту BD.
По
свойству
равнобедренного треугольника:
высота, проведенная к основанию так же является и
медианой.
Следовательно, AD=DC=AC/2=30/2=15
Чтобы вычислить эту высоту треугольника воспользуемся
теоремой Пифагора:
AB2=BD2+AD2
252=BD2+152
625=BD2+225
BD2=400
BD=20
Площадь треугольника: S=ah/2=AC*BD/2
S=30*20/2=300
Ответ: S=300
Поделитесь решением
Присоединяйтесь к нам...
В параллелограмме ABCD диагонали AC и BD пересекаются в точке M. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BMC.
 У треугольника со сторонами 4 и 16 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне?
У треугольника со сторонами 4 и 16 проведены высоты к этим сторонам. Высота, проведённая к первой стороне, равна 4. Чему равна высота, проведённая ко второй стороне?
 В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
В треугольнике ABC угол C равен 90°, sinA=0,4, AC=√
 Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
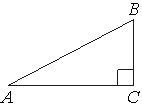 В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.
В треугольнике ABC угол C равен 90°, BC=3, AB=5. Найдите cosB.

Комментарии: