
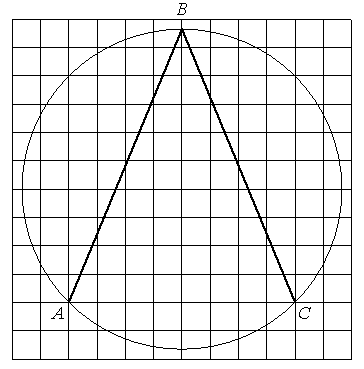
 Найдите угол ABC. Ответ дайте в градусах.
Найдите угол ABC. Ответ дайте в градусах.
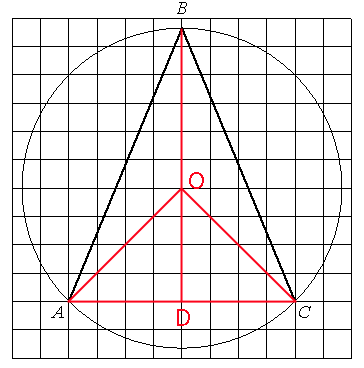 Проведем отрезки как показано на рисунке. Точка О - центр окружности
Проведем отрезки как показано на рисунке. Точка О - центр окружности
Рассмотрим треугольник AOD.
Данный треугольник
прямоугольный, так как ∠ODA=90°
AD=OD=4, следовательно треугольник AOD -
равнобедренный.
По
теореме о сумме углов треугольника:
180°=∠ODA+∠DAO+∠AOD
180°=90°+∠DAO+∠AOD
90°=∠DAO+∠AOD
А так как ∠DAO=∠AOD (по
свойству равнобедренного треугольника), то:
∠DAO=∠AOD=90°/2=45°.
Рассмотрим треугольники AOD и COD.
AD=CD=4
OD=4 - общая сторона.
∠ODA=∠ODC=90°
Тогда, по
первому признаку равенства треугольников, данные треугольники равны.
Следовательно, ∠AOD=∠COD=45°
∠AOC=∠AOD+∠COD=45°+45°=90°
∠AOC - является
центральным для окружности, следовательно градусная мера дуги, на которую опирается этот угол тоже равна 90°.
∠ABC - является
вписанным в окружность и опирается на ту же дугу. Следовательно, по
свойству угла, он равен половине градусной меры дуги. ∠ABC=90°/2=45°.
Ответ: 45
Поделитесь решением
Присоединяйтесь к нам...
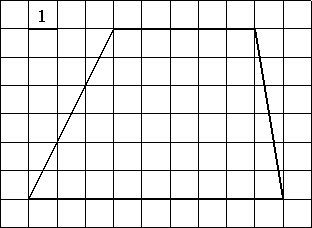 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
Основание AC равнобедренного треугольника ABC равно 6. Окружность радиуса 4,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 Найдите площадь квадрата, описанного около окружности радиуса 32.
Найдите площадь квадрата, описанного около окружности радиуса 32.

Комментарии: