Касательные к окружности с центром O в точках A и B пересекаются под углом 82°. Найдите угол ABO. Ответ дайте в градусах.
Проведем отрезок CO.
Рассмотрим треугольник ACO.
∠ACO=∠ACB/2=82°/2=41° (по
второму свойству касательной).
∠CAO=90° (по
первому свойству касательной)
По
теореме о сумме углов треугольника:
180°=∠AOC+∠ACO+∠CAO
180°=∠AOC+41°+90°
∠AOC=49°
Рассмотрим треугольники ACO и BCO.
OC - общая сторона
AC=BC (по
второму свойству касательной)
OA=OB (т.к. это радиусы)
Следовательно, по
третьему признаку, данные треугольники равны.
Тогда и ∠AOC=∠BOC=49°
Рассмотрим треугольник AOB.
OA=OB (т.к. это радиусы)
Следовательно, треугольник AOB -
равнобедренный.
Тогда ∠BAO=∠ABO (по
свойству равнобедренного треугольника).
По
теореме о сумме углов треугольника:
180°=∠AOB+∠OAB+∠ABO
180°=∠AOC+∠BOC+2∠ABO
180°=49°+49°+2∠ABO
82°=2∠ABO
∠ABO=41°
Ответ: 41
Поделитесь решением
Присоединяйтесь к нам...
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
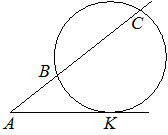Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=4, AC=64. Найдите AK.
В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKB.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=18, DK=9, BC=16. Найдите AD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: