В трапеции ABCD AB=CD, AC=AD и ∠ABC=95°. Найдите угол CAD. Ответ дайте в градусах.
Так как AB=CD, значит трапеция ABCD -
равнобедренная.
Тогда по
свойству равнобедренной трапеции ∠ABC=∠BCD=95° и ∠CDA=∠DAB.
Вспомнив, что сумма углов выпуклого n-угольника вычисляется по формуле (n-2)180°, получим, что сумма углов трапеции равна (4-2)180°=360°.
Тогда ∠ABC+∠BCD+∠CDA+∠DAB=360°
95°+95°+∠CDA+∠DAB=360°
∠CDA+∠DAB=170°
∠CDA=∠DAB=170°/2=85°
Рассмотрим треугольник ACD.
Так как AC=AD, то данный треугольник -
равнобедренный.
Следовательно, по
свойству равнобедренного треугольника ∠CDA=∠DCA=85°
∠BCA=∠BCD-∠DCA=95°-85°=10°
∠CAD=∠DCA=10° (т.к. они
накрест-лежащие для параллельных прямых AD и BC).
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
Точка H является основанием высоты, проведённой из вершины прямого угла B треугольника ABC к гипотенузе AC. Найдите AB, если AH=6, AC=24.
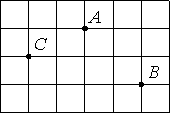На клетчатой бумаге отмечены точки A, B и C. Площадь одной клетки равна 1. Найдите расстояние от точки A до середины отрезка BC.
Стороны AC, AB, BC треугольника ABC равны 2√
В треугольнике ABC угол C равен 90°, sinA=8/9, AC=2√
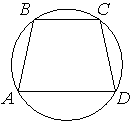Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: