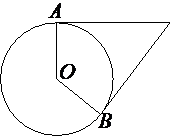
Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
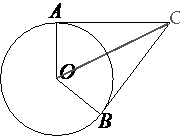Проведем отрезок ОС, как показано на рисунке.
Треугольники ACO и BCO -
прямоугольные (по
свойству касательной).
То есть углы CAO и CBO равны по 90° каждый.
OC - является
биссектрисой для угла ACB (по
свойству касательных), следовательно углы ACO и BCO равны 6°/2=3°.
По
теореме о сумме углов треугольника, для треугольника ACO запишем:
180°=∠OAC+∠ACO+∠COA
180°=90°+3°+∠COA
∠COA=180°-90°-3°=87°
Аналогично, для треугольника BCO получим, что ∠COB=87°
∠AOB=∠COA+∠COB=87°+87°=174°
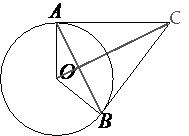Проведем отрезок AB и рассмотрим треугольник ABO.
По
теореме о сумме углов треугольника запишем:
180°=∠AOB+∠BAO+∠ABO
180°=174°+∠BAO+∠ABO
∠BAO+∠ABO=6°
ABO
равнобедренный треугольник, т.к. OA и OB - радиусы окружности и, поэтому, равны. Следовательно ∠ABO=∠BAO (по
свойству равнобедренного треугольника). И получается, что ∠ABO=∠BAO=6°/2=3°
Ответ: ∠ABO=3°
Поделитесь решением
Присоединяйтесь к нам...
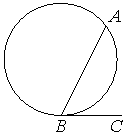На окружности отмечены точки A и B так, что меньшая дуга AB равна 152°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
На стороне BC прямоугольника ABCD, у которого AB=12 и AD=17, отмечена точка E так, что
/EAB=45°. Найдите ED.
Центральный угол
AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
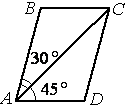Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-06 22:51:21) Администратор: Елена, по сути это тоже самое, что и в решении, только я отталкиваюсь от суммы углов треугольника (что знает большинство школьников), Вы отталкиваетесь от суммы углов четырехугольника (что знают далеко не все школьники).
(2015-04-06 18:59:36) Елена: В четырёхугольнике АСВО уголы А и В прямые, угол С равен 6 градусов. Сумма углов четырёхугольника 360 градусов, значит угол О равен 174 градуса. А дальше по теореме о сумме углов треугольника...