В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
Так как, по условию, AB=BC, то данный треугольник называется равнобедренным.
По
первому свойству равнобедренного треугольника углы, противолежащие равным сторонам, равны между собой (обозначим их α).
Тогда по теореме о сумме углов треугольника:
180°=∠ABC+∠BCA+∠CAB
180°=122°+∠α+∠α
180°-122°=2∠α
58°=2∠α
∠α=58°/2=29°
Ответ: 29
Поделитесь решением
Присоединяйтесь к нам...
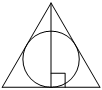Радиус окружности, вписанной в равносторонний треугольник, равен 12. Найдите высоту этого треугольника.
В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Найдите площадь квадрата, описанного около окружности радиуса 32.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: