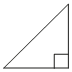
В прямоугольном треугольнике один из катетов равен 7, а острый угол, прилежащий к нему, равен 45°. Найдите площадь треугольника.
По
теореме о сумме углов треугольника можно вычислить третий угол, он равен 180°-90°-45°=45°.
Следовательно, этот треугольник
равнобедренный (по первому
свойству).
Т.е. катеты этого треугольника равны.
Площадь
прямоугольного треугольника = ab/2, где а и b - катеты. Тогда:
Sтреугольника=7*7/2=24,5
Ответ: Sтреугольника=24,5
Поделитесь решением
Присоединяйтесь к нам...
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=15° и ∠OAB=8°. Найдите угол BCO. Ответ дайте в градусах.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите расстояние от точки А до точки О, если угол между касательными равен 60°, а радиус окружности равен 8.
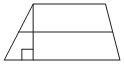Основания трапеции равны 2 и 6, а высота равна 3. Найдите среднюю линию этой трапеции.
Найдите угол, который образуют минутная и часовая стрелки часов в 11:00. Ответ дайте в градусах.
Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: