В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=84 и BC=BM. Найдите AH.
Так как BM -
медиана, значит AM=MC=AC/2=84/2=42
Рассмотрим треугольник MBC.
Т.к. BC=BM (по условию задачи), значит этот треугольник
равнобедренный, BH -
высота этого треугольника. По
третьему свойству равнобедренного треугольника MH=HC=MC/2=42/2=21
Искомая AH=AC-HC=84-21=63
Ответ: AH=63
Поделитесь решением
Присоединяйтесь к нам...
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 120°, а CD=34.
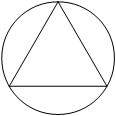Сторона равностороннего треугольника равна 2√
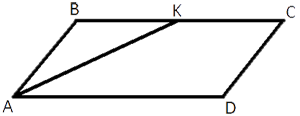Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
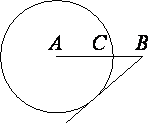На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Площадь прямоугольного треугольника равна 18√
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: